Research
Our research interests focus on the study of complex systems and
soft matter physics. This involves the modelling of various
physical & biological systems, using dynamical systems
theory and methods. Problems we are interested in cover a large
range of topics, solving which involves a multi-disciplinary
approach, using concepts from various fields of physics. A
typical system of interest would be a complex physical system,
with an interplay of interactions at different scales, both
spatial and temporal. Examples of systems that we are
investigating are given below. These range from living systems
at the nano and micro metre scale to physical systems like
oceans at several hundred kilometres. Brief summaries of some of
the topics of our research follow.Instabilities in flows at small scales and in living systems
Some of our recent work investigates instabilities in flows in living systems. We are interested in learning about & predicting the behaviour of microfluidic flows under various conditions & control parameter values. The effects of geometry & external fields are being studied. The focus of research is on flows in both living systems as well as at nanometre and micrometre regimes in the context of practical applications.
Nonlinearities in mechanical systems
Mechanical systems have long been a subject of study in nonlinear dynamics. We continue our work in that tradition
but with the motivation that mechanistic analogues of real-life living and physical systems can provide a deep, intuitive understanding of the working of very complex systems and the physical principles underlying them.
An earlier, related work involved modelling double-walled carbon nanotubes (DWCNTs) and considering their behaviour in the context of their uses as nanoscale nonlinear springs, nano-gears, ratchets and bearings. Good agreement was found between our mechanistic model and theresults obtained from quantum-mechanical density functional theory calculations for the system.
Bubble dynamics & cavitation
Another
problem under study is that of bubble dynamics and
cavitation in fluids. This occurs in various
situations & is associated with various phenomena,
ranging from the cavitation damage to propellers of
ships, single and multi-bubble sonoluminescence,
forced bubble oscillations in living tissue,
shock-wave generation and cavitation by living
organisms such as shrimps, the sound associated with
running water: the list goes on and on. A forced
oscillating bubble in a fluid is a very rich nonlinear
system showing very surprising and interesting
behaviour. We study the dynamics of such a
system, under acoustic forcing, using a modified
Rayleigh-Plesset equation, investigating the effect of
various physical parameters. Our recent work has
focused on charged bubbles, investigating charge &
pressure thresholds.
Living things depend upon their various senses for their survival. Sensory cells detecting different modalities have developed sophisticated mechanisms to convey the various features of the external environment to the living system in the shortest possible time. The essential nonlinearities inherent in the signal transduction mechanism can take advantage of the noise from the environment the system is subject to, to display a highly amplified response to stimuli in a frequency-selective manner. We study the role of the Hopf bifurcation in detection of stimuli in sensory processes.
Studies of neuronal firing behaviour include investigations of neuron models as flows & maps, constructing models that replicate observed bursting behaviour, and understanding the dynamics of neuronal firing from a dynamical systems theory point of view.
Modelling climate phenomena
Dynamical instabilities, noise & sensory detection
Living things depend upon their various senses for their survival. Sensory cells detecting different modalities have developed sophisticated mechanisms to convey the various features of the external environment to the living system in the shortest possible time. The essential nonlinearities inherent in the signal transduction mechanism can take advantage of the noise from the environment the system is subject to, to display a highly amplified response to stimuli in a frequency-selective manner. We study the role of the Hopf bifurcation in detection of stimuli in sensory processes.
Synchronization in
nonlinear systems
We are also interested in the synchronization behaviour of nonlinear systems. Addition of weak noise may cause synchronization to occur in some systems. We have studied noise-induced synchronization in a system of coupled nonlinear oscillators which exhibit self-sustained oscillations.
We are also interested in the synchronization behaviour of nonlinear systems. Addition of weak noise may cause synchronization to occur in some systems. We have studied noise-induced synchronization in a system of coupled nonlinear oscillators which exhibit self-sustained oscillations.
Dynamics of coupled neurons
Studies of neuronal firing behaviour include investigations of neuron models as flows & maps, constructing models that replicate observed bursting behaviour, and understanding the dynamics of neuronal firing from a dynamical systems theory point of view.
Modelling climate phenomena
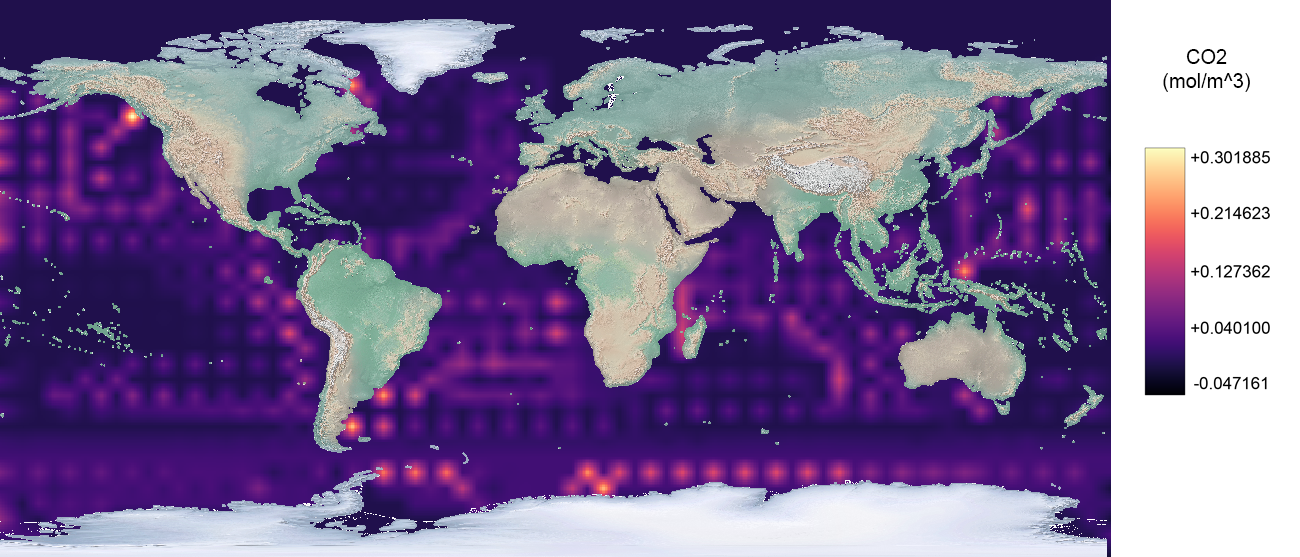
This includes some recent work on
ocean carbon sinks & climate change,
which is expected to have a strong impact in
understanding climate dynamics. Our work focuses on
predicting the location & the spatio-temporal
evolution of ocean carbon sinks and its influence on
climate change. Our model's results &
predictions seem to be in agreement with known data
(present climate patterns as well as paleoclimate).
We predict the evolution of the aqueous carbon
dioxide absorbed by the world's oceans as a function
of time and spatial location.
Other work includes construction of mathematical models that qualitatively capture the behaviour of complex climate phenomena such as tropical precipitation.
Modelling ecological systems
Another problem we have been working on involves modelling the effects of climate change on ecological systems & populations and some interesting results have been obtained.Vesicular
nanotubulation
An interesting problem, one
motivated by nanotubulation experiments concerns the
dynamics 
of
vesicle-pulling. This phenomenon of nanotube formation has
practical applications – e.g., the formation of networks of
nanotubes and containers that can be formed through mechanical
excitation of vesicles, useful in making nanofluid devices
& drug delivery systems. We have theoretically
investigated the dynamical behaviour of a vesicle
attached to a substrate and pulled with a constant velocity.
We have considered the effects of change in vesicular geometry
and various dissipative effects that come into play as
the lipid layers are pulled out to form a nanotube. Our
theoretical model is in substantial qualitative agreement with
experimental observations.
Another problem of interest is the theoretical investigation of the behaviour of combustion growth fronts under various conditions. Phenomena like fingering instabilities & effect of geometry on the combustion dynamics are sought to be understood.
Other problems of interest:
of
vesicle-pulling. This phenomenon of nanotube formation has
practical applications – e.g., the formation of networks of
nanotubes and containers that can be formed through mechanical
excitation of vesicles, useful in making nanofluid devices
& drug delivery systems. We have theoretically
investigated the dynamical behaviour of a vesicle
attached to a substrate and pulled with a constant velocity.
We have considered the effects of change in vesicular geometry
and various dissipative effects that come into play as
the lipid layers are pulled out to form a nanotube. Our
theoretical model is in substantial qualitative agreement with
experimental observations.
Instabilities in combustion
Another problem of interest is the theoretical investigation of the behaviour of combustion growth fronts under various conditions. Phenomena like fingering instabilities & effect of geometry on the combustion dynamics are sought to be understood.
Other problems of interest:
- Quantum computing with nonlinear oscillator networks (project funded by Mphasis under the auspices of the Mphasis Center for Cognitive Computing, IIIT Bangalore)
- There are various other research problems that are of interest to us that we have worked on including:
- Problems in complex fluids and constrained flows
- Physics of polymeric & polyelectrolytic systems
- Applications of concepts of statistical physics in search and optimization problems